Answers

Functions

    1. 2;
    2. 2;
    3. 1.
    1. $3\times 2 - 5x$;
    2. $10\times2$;
    3. $e^{4x}$.
    1. $f(x, y)$ simplifies to 1.
      $x$ $y$ $f(x,y)$
      1 1 1
      1 0 1
      0 1 1
      0 0 0
    2. $f(x, y)$ simplifies to $y'.$
      $x$ $y$ $f(x,y)$
      0 0 1
      1 0 1
      0 1 0
      1 1 0
      $f(x, y)$ simplifies to $xy$ here.
    3. $x$ $y$ $f(x,y)$
      0 0 0
      1 0 0
      0 1 0
      1 1 1
    4. $f(x, y)$ simplifies to $xy'$.
      $x$ $y$ $f(x,y)$
      0 0 0
      1 0 1
      0 1 0
      1 1 0
    5. $f(x, y)$ simplifies to $x + y$.
      $x$ $y$ $f(x,y)$
      0 0 0
      1 0 1
      0 1 1
      1 1 1
    1. $x$ $y$ $z$ $f(x,y,z)$
      0 0 0 0
      0 1 0 0
      0 0 1 0
      0 1 1 1
      1 0 0 0
      1 1 0 1
      1 0 1 1
      1 1 1 1

      Why do we get that answer? Is it because the expression simplifies to something simple? If so, what?

    2. $x$ $y$ $z$ $f(x,y,z)$
      0 0 0 0
      0 1 0 1
      0 0 1 1
      0 1 1 1
      1 0 0 1
      1 1 0 1
      1 0 1 1
      1 1 1 1

    Why do we get that answer? What does the expression simplify to?

  5. In a Boolean algebra, $x^2 = x \times x = x$. So every power of an element reduces to the original element. Hence there are no powers in a polynomial function. On the other hand $x \times x' = 0$, so there are no possible products of the form $xx'$. There are no other possibilities for the potential powers and products of $x$ and $x'$ so $f(x) = \alpha x + \beta x'$. This assumes that there are no constants. Any non-zero constant has to be 1 which would make the function equivalent to 1.

    The coefficients $\alpha$ and $\beta$ must come from the Boolean algebra in question. But we can be more precise than this. Now $f(0) = \alpha\times 0 + \beta \times 1 = \beta$ and similarly $f(1) = \alpha$. So $f(x) = f(1) x + f(0) x'$.

  6. The answer here is similar to that in Q40, but we have more combinations of variables. The constants can be defined in terms of f(0, 0), f(0, 1), f(1, 0) and f(1, 1).

    Three variables is a little more messy because it will have more terms. But the coefficients can be found in the same way via terms like $f(1, 0, 1)$.

    1. $f(x, y) = xy$, so we need two switches in series.
    2. $f(x, y, z) = xy + z(xy' + x'y)$.
    3. $f(w, x, y, z) = wxy + wxz + wyz + xyz$.
    4. $f(w, x, y, z) = wx$, $w$ and $x$ represent Able and Baker.
  8. $f(x, y) = xy' + x'y$.
  9. $f(x, y, z) = xyz + xy'z' + x'yz' + x'y'z.$
  10. Only (xii) is a proposition because it is the only one that is a statement that can be given a value of true (1) or false (0). In particular exclamations (viii), questions (ix), and declamations (x) can never be propositions. On the other hand, (xii) is a statement about peas. For some peas the statement may be true and for others it may be false. So (xii) is a proposition.

    But (xi) is a worry. If the sentence is false then it has to be true, and if the sentence is true it is false. So (xi) can't be assigned either 0 or 1. The self-reflective nature of this sentence is a hurdle against it being a proposition. But 'this sentence is true' is a proposition because it can be given the truth value T (1). And 'this other sentence is false' is also a proposition, because it can be true or false depending on the other sentence. So you have to tread carefully with propositions. A small word change can mean a great difference.

    1. These lines are not parallel;
    2. This angle is not 30$^{\circ}$;
    3. Jake doesn't have a knife;
    4. Jake didn't kill the victim;
    5. Not all men are liars (but not all men are not liars);
    6. Helen is not a liar;
    7. Helen is not a man;
    8. These peas are not horrible.
  12. pq: (i), (iii), (v), (vi) (black and dog). $p + q$: (ii) (iv). The 'and' and the 'or' usually give the game away.
    1. Alex swam at the Olympics and won a gold medal;
    2. Alex swam at the Olympics or won a gold medal;
    3. Alex swam at the Olympics and didn't win a gold medal;
    4. Alex swam at the Olympics or didn't win a gold medal;
    5. Alex swam at the Olympics or didn't swim at the Olympics and won a gold medal;
    6. Alex didn't swim at the Olympics and won a gold medal or did swim at the Olympics and didn't win a gold medal.
    1. $p$ $q$ $q'$ $pq$
      0 0 1 0
      0 1 0 0
      1 0 1 1
      1 1 0 0
    2. $p$ $q$ $q'$ $pq$
      0 0 1 1
      0 1 0 0
      1 0 1 1
      1 1 0 1
    3. $p$ $p'$ $q$ $p'q$ $p + p'q$
      0 1 0 0 0
      0 1 1 1 1
      1 0 0 0 1
      1 0 1 0 1

      Note that $p + p'q$ is the same as $p + q$. Why might this be the case?

    4. $p$ $p'$ $q$ $q'$ $p'q$ $pq'$ $p'q + pq$
      0 1 0 1 0 0 0
      0 1 1 0 1 0 1
      1 0 0 1 0 1 1
      1 0 1 0 0 0 0
  15. This will depend on what you have written.
    1. (i) only false if $p = 0 = q$;
    2. (ii) only false if $p = q = 1$ and $r = 0$;
    3. (iii) only false if $p = 0$ and $q = 1$;
    4. (iv) only false if $p = q = 0$ and$ p = 1$ and $q = 0$;
    5. (v) always true.
  17. This is false for $p = 1$ and $q = 0$ and $p = 1$ and $q = 0$.
  18. Try $p'+ q$.
  19. (i), (ii), (iii), (iv) are tautologies but the last two are not.
    1. Let $p = $it rains and $q = $ roof wet. Now $q \to p$ is not a tautology so the conclusion is false.
    2. Although a 3, 4, 5 triangle is right angled it cannot be proved using this argument because it is not a tautology;
    3. Let $p =$ right angled triangle and $q = a^2 + b^2 + c^2$. Does $(p \to q) \to (q' \to p')$? This is a tautology, so the 3, 4, 6 triangle is not a right angled one.\\
  21. Again the truth tables of $pq$ and $qp$ are the same.
  22. The truth tables for all of the axioms do what you hope they would do.
  23. See Q53.
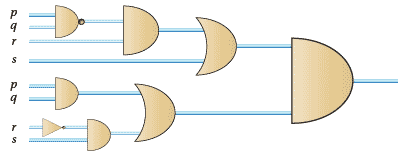
  24. The circuits are shown below.

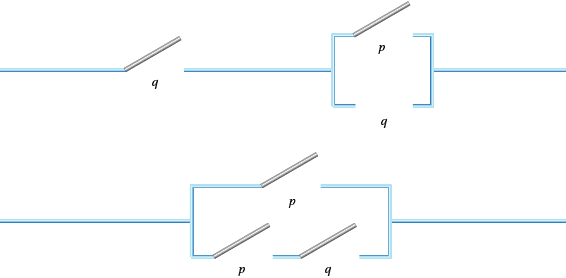
    The equivalence can be shown using truth tables or Boolean algebra.

    1. a $(p'q + r)'\hspace{20px}$b $(p'q'+ r)s$.
    2. The table for Q42(c) is
      $w$ $x$ $y$ $z$ vote
      0 0 0 0 0
      0 0 0 0 1
      0 0 0 1 0
      0 0 1 0 0
      0 1 0 0 0
      0 1 1 0 0
      0 1 1 1 1
      1 0 0 0 0
      1 0 0 1 1
      1 0 1 1 1
      1 1 0 1 1
      1 1 1 0 1
      1 1 1 1 1

      One corresponding K-map is shown below.

      $x$ $yz$
        00 01 11 10
      00 0 0 0 0
      01 0 0 1 0
      11 0 1 1 1
      10 0 0 1 0

      Going along the third row gives \[wxy'z + wxyz = wxz \mbox{ and } wxyz + wxyz'= wxy;\]

      going down the third column gives \[w'xyz + wxyz = xyz \mbox{ and } wxyz + wx'yz = wyz\]

      The combined result is $wxy + wxz + wyz + xyz$. Check this with the answer in Q42(c).

  27. The K-map can be written straight from the proposition.
    $p$ $qr$
      00 01 11 10
    0 1 1 1 0
    1 1 1 1 1

    The first row gives: \[p'q'r'+ p'q'r = p'q' \mbox{ and } p'q'r + p'qr = p'r\]

    The second row gives:\[pq'r'+ pq'r = pq', pq'r + pqr = pr, and pqr + pqr' = pq.\] But as the row contains four ones we can get a simplification more quickly. Since $p$ remains 1 throughout and $q$ and $r$ change from 0 to 1, then the whole row reduces to $p$. (Check that $pq'+ pr + pq = p$ using Boolean algebra.)

    The columns give: $q'r', q'r$ and $qr$.

    Altogether this simplifies to $p + q'+ r$.

    But this can be done more efficiently by noting that we have several $2 \times 2$ rectangles of ones. The first one consists of columns 1 and 2 and rows 1 and 2. As a result, this block simplifies to $q'$ as this is the only term that is unchanged throughout the block. Similarly the only constant term in the block made up of columns 2 and 3 and rows 1 and 2. The only constant term here is $r$. Then row 2 is also constant on $p$. This method produces $p + q' + r$ much more efficiently than the adjacent terms method above.

    $pq$ $rs$
      00 01 11 10
    00 0 1 0 0
    01 0 1 0 0
    11 0 1 1 0
    10 0 1 0 0

    The second column is a block of four and so gives a simplification of $r's$.

    The second and third columns of the third row gives $pqs$.

    Overall this gives $s(r' + pq)$.

  28. By the K-map approach, since $x$ and $z$ are the only terms that are all 1 in the 2 x 2 square, and the other terms are both 0 and 1, we get $xz$.

    By the disjunctive normal form we get $w'xy'z + w'xyz + wxy'z + wxyz$. Now the first two terms together give $w'xz$ and the last two give $wxz$. Then $w'xz + wxz = xz$ as Karnaugh predicts.